无动力风帽又叫球形通风器，是屋顶常见的一种通风设备。一风帽如图所示，它会在自然风的推动下绕其竖直中心轴旋转。在其边缘某处粘有一块质量为$m$的橡皮泥，过橡皮泥所处的位置的一条切线竖直，橡皮泥到中心轴的距离为$l$。某段时间内，风帽做匀速圆周运动，在时间$t$内发现风帽旋转了$n$圈。重力加速度大小为$g$。求：$(1)$橡皮泥向心加速度的大小；$(2)$风帽对橡皮泥作用力的大小。

（1）设橡皮泥随风帽一起运动的角速度为$\omega $，则$ω=\frac{2nπ}{t}$，橡皮泥的向心加速度$a_{n}=\omega ^{2}l=(\frac{2nπ}{t})^{2}l=\frac{4{n}^{2}{π}^{2}l}{{t}^{2}}$；

$(2)$橡皮泥运动时的向心力$F_{n}=m\omega ^{2}l$，

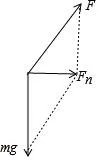
对橡皮泥受力分析可知：风帽对橡皮泥的作用力$F=\sqrt{(mg)^{2}+{F}_{n}^{2}}$

联立解得：$F=m\sqrt{{g}^{2}+\frac{16{π}^{4}{n}^{4}{l}^{2}}{{t}^{4}}}$

答：（1）橡皮泥向心加速度的大小为$\frac{4{n}^{2}{π}^{2}l}{{t}^{2}}$；

$(2)$风帽对橡皮泥作用力的大小为$m\sqrt{{g}^{2}+\frac{16{π}^{4}{n}^{4}{l}^{2}}{{t}^{4}}}$。